Bihar Board Class 10 Maths Solutions Chapter 11 रचनाएँ Ex 11.1

प्रश्न 1. 7.6 cm लम्बा एक रेखाखण्ड खींचिए और इसे 5 : 8 के अनुपात में विभाजित कीजिए। दोनों भागों को मापिए।

 

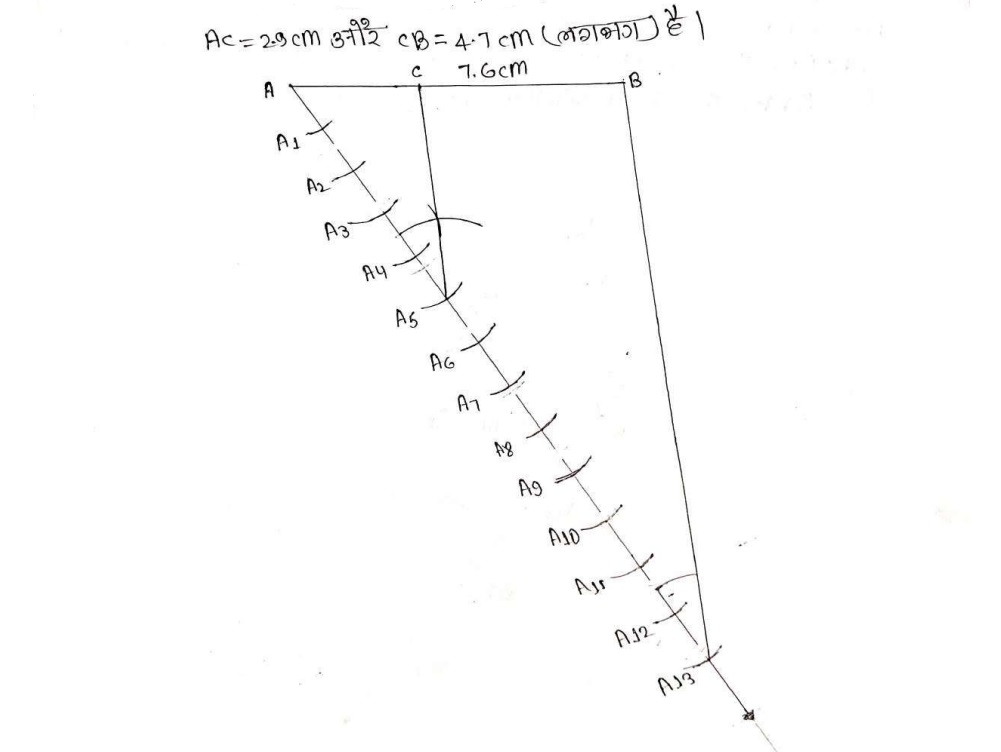
रचना के चरण :
(i) AB = 7.6 cm का एक रेखाखंड खीचा ।
(ii) रेखाखंड AB से न्‍युनकोण बनाती हुई कोई किरण Ax खीचा ।
(iii) किरण Ax पर 13 (=m+nie. 13 = 5 + 8) बिन्‍दु A₁, A_2,, A₃, A₄, A₅, A₆, A₇, A₈, A₉, A₁₀, A₁₁, A₁₂ और A₁₃ इस प्रकार अंकित किया कि AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇ = A₇A₈ = A₈A₉ = A₉A₁₀ = A₁₀A₁₁ = A₁₁A₁₂ = A₁₂A₁₃ हो ।
(iv) BA₁₃ को मिलाया ।
(v) बिंदु A₅ (m = 5) से होकर जाने वाली A₁₃ B के समांतर एक रेखा बिंदु A₅ पर <AA₁₃ B के बराबर कोण बनाकर, AB को बिंदु C पर प्रतिछेद करती हुई खीचा जैसा कि उपर्युक्त आकृति में दर्शाया गया हैं। तब AC:CB = 5 है। दोनो भागों को मापने पर आते है कि AC = 2.9 cm और CB = 4.7cm (लगफग) है ।  

प्रश्न 2. 4 cm, 5 cm और 6 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की `\frac{2}{3}` गुनी हों।

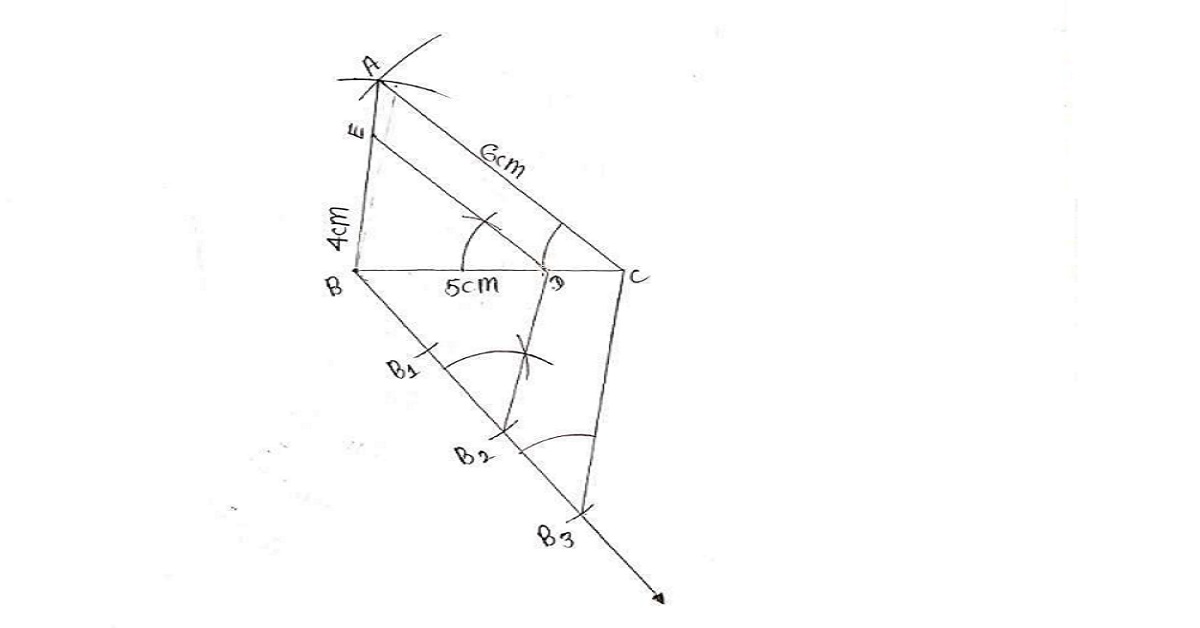
रचना के चरण :

(i) रेखाखंड AB = 6 cm खीचा ।

(ii) बिंदु A को केन्‍द्र मानकर 4 cm त्रिज्‍या लेकर एक चाप खीचा ।

(iii) अब, बिंदु B को केन्‍द्र मानकर 5 cm त्रिज्‍या लेकर एक अन्‍य चाप खींचा जो चरण 2 वाले चाप को माना बिंदु C पर प्रतिछेद करता है।

(iv) AC और BC को मिलाया । इस प्रकार हमें ABC एक त्रिभुज प्राप्‍त हुआ जिसकी भुजा 6cm, 5cm, और 4cm है।

(v) रेखाखंड AB के निचे एक न्‍युन कोण बनाती हुई किरण AX खींचा ।

(vi) किरण AX पर 3 बिन्‍दु (2/3 में 2 और 3 में से बड़ी संख्‍या) A₁, A₂ और A₃ इस प्रकार अंकित किया कि AA₁ = A₁A₂ = A₂A₃ हो ।

(vii) A₃B को मिलाकर A₂ (दूसरा बिंदु यहाँ `\frac{2}{3}` में 2 और 3 में से सबसे छोटी संख्‍या) से होकर जाने वाली A₃B के समांतर एक रेखा खींचा जो AB को किसी बिंदु B पर प्रतिच्‍छेद करती है ।

(viii)  B से होकर जाने वाली BC के समांतर एक रेखा खींचा जो AC को बिंदु C पर प्रतिच्‍छेद करती हैं।
तब ∆ABC ही अभीष्‍ट समरूप त्रिभुज है जिस प्रत्‍येक भुजा दिए हुए ∆ABC की संगत भुजाओं की `\frac{2}{3}` गुणी हैं।

प्रश्न 3. 5 cm, 6 cm और 7 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की `\frac{7}{5}` गुनी हों।

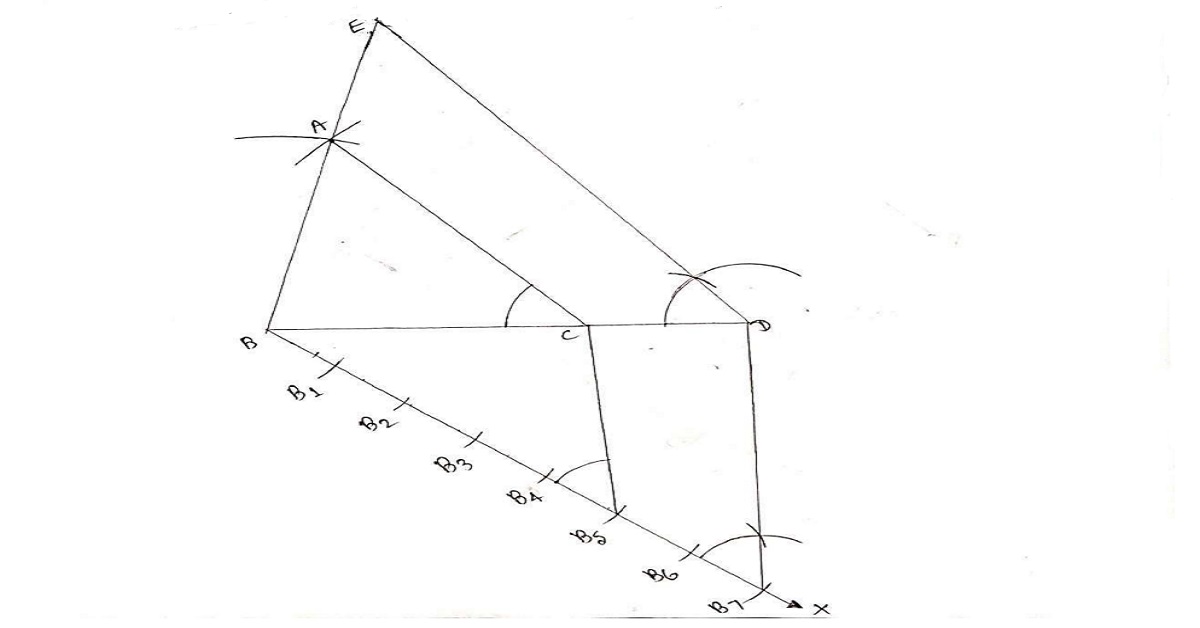
रचना के चरण : 

(i) रेखाखंड BC = 7 cm खीचा ।

(ii) बिंदु B को केन्‍द्र मानकर और 5 cm त्रिज्‍या लेकर एक चाप खींचा ।  

(iii) बिंदु C को केन्‍द्र मानकर और 6 cm त्रिज्‍या लेकर एक अन्‍य चाप खींचा जो चरण 2 वाले चाप को माना बिंदु A पर प्रतिच्‍छेद करता है।

(iv) AB और AC को मिलाया । इस प्रकार हमें ∆ABC अभीष्‍ट त्रिभुज प्राप्‍त होता है जिसकी भुजाएँ 5cm, 7cm और 6cm हैं।

(v) रेखाखंड BC के निचे एक न्‍युन कोण बनाती हुई कोई किरण BY खीचा ।

(vi) किरण BY पर बिंदु (`\frac{7}{5}` में 7 और 5 में बड़ी संख्‍या) B₁, B_2,, B₃, B₄, B₅, B₆, और B₇ इस प्रकार अंकित किया की कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇ हो ।

(vi) किरण BY पर बिंदु (`\frac{7}{5}` में 7 और 5 में बड़ी संख्‍या) B₁, B_2,, B₃, B₄, B₅, B₆, और B₇ इस प्रकार अंकित किया की कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇ हो ।

(vii) B₅ (पाँचवाँ बिंदु `\frac{7}{5}`में 7 और 5 में से छोटी संख्‍या) को C से मिलाया और B₇ से होकर जाने वाली B₅C एक रेखा खींच जो अढ़ाए गए रेखाखंड BC को माना C पर प्रतिच्‍छेद करती हैं।

(viii) C से होकर जाने वाली CA के समांतर एक रेखा बढ़ाए गए रेखाखंड  BA के मान A पर प्रतिच्‍छेद करती हुई खीचा ।
तब हमें ABC अभीष्‍ट त्रिभुज प्राप्‍त होता है जो दिए हुए ∆ABC के प्रत्‍येक संगत भुजाओं के `\frac{7}{5}` गुणी हैं।

प्रश्न 4. आधार 8 cm तथा ऊँचाई 4 cm के एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ इस समद्विबाहु त्रिभुज की संगत भुजाओं की `1\frac{1}{2}` गुनी हों।

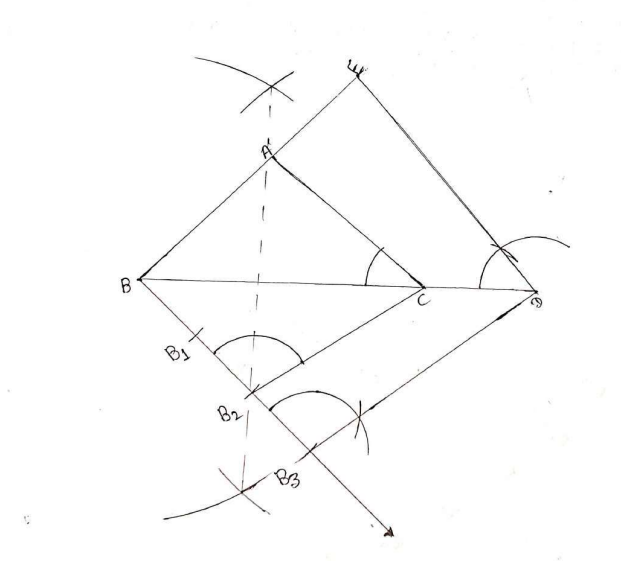
रचना के चरण : 

(i) रेखाखंड BC = 8cm खीचा और इसके समद्विभजित किया 1 माना बिंदु D, BC के मध्‍य बिंदु हैं।

(ii) बिंदु D को केंद्रे मानकर और दी हुई ऊँचाई 4 cm का चाप खींचा जो BC के लंब समद्विभाजको, माना किसी बिंदु A पर प्रतिच्‍छेद करता हैं।

(iii) AB और AC को मिलाया । इस प्रकार हमें ABC एक समद्विबाहु त्रिभुज प्राप्‍त हुआ । जिसका आधार 8cm और ऊँचाई 4cm हैं।

(iv) अब BC को किसी बिंदु C तक इस प्रकार बढ़ाया कि BC (`1\frac{1}{2}` BC = `\frac{3}{2}`×8 = 12cm हो ।

(v)  बिंदु C से CA||CA खींचा जो बढ़ाए गए BA को माना बिंदु A पर प्रतिच्‍छेद करती हैं। तब ∆ABC ही अभीष्‍ट समद्विबाहु त्रिभुज है जिसकी प्रत्‍येक भुजा ∆ABC की संगत भुजाओं की `1\frac{1}{2}` = `\frac{3}{2}`

प्रश्न 5. एक त्रिभुज ABC बनाइए जिसमें BC = 6 cm, AB = 5 cm और ∠ABC = 60° हो। फिर एक त्रिभुज की रचना कीजिए जिसकी भुजाएँ ∆ABC की संगत भुजाओं की `\frac{3}{4}` गुनी हों।

रचना के चरण : 

(i) रेखाखंड BC = 6cm खींचा ।

(ii) बिंदु B पर 60­­­⁰ का कोण CBY बनाया ।

(iii) किरण BY में AB = 5cm का चाप काटा जिससे AB = 5cm हैं।

(iv) AC को मिलाया । इस प्रकार हमे ∆ABC प्राप्‍त हुआ ।

(v) अब BC के नीचे न्‍यून कोण बनाती हुई एक किरण BX खींचा ।

(vi) किरण BX पर 4 बिंदु (`\frac{3}{4}` में 3 और 4 बड़ी संख्‍या) B₁, B_2,, B₃ और B₄ इस प्रकार अंकित किया कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ हो ।

(vii) B₄C को मिलया और B₃ (तिसरे बिंदु `\frac{3}{4}` में 3 और 4 में से छोटी संख्‍या) से B₄C के समांतर एक रेखा खींचा जो BC को माना C पर प्रतिच्‍छेद करती हैं।

(viii) अब C से CA||CA खींचा जो BC को मान C पर प्रतिच्‍छेद करती है।
तब ∆ABC ही अभीष्‍ट त्रिभुज है जिसकी प्रत्‍येक भुजा दी हुई ∆ABC की संगत भुजाओं की `\frac{3}{4}` गुणी हैं।

प्रश्न 6. एक त्रिभुज ABC बनाइए जिसमें BC = 7 cm, ∠B = 45° व ∠A = 105° हो। फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ ∆ABC की भुजाओं की `\frac{4}{3}` गुनी हों।

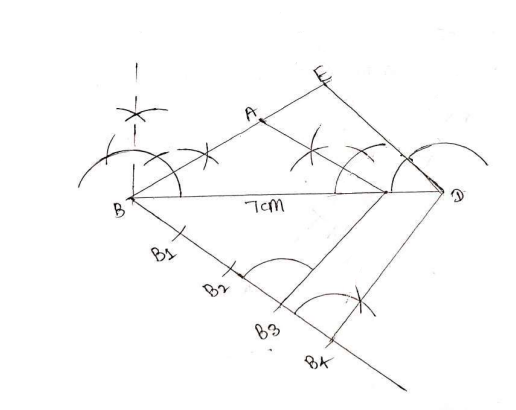
रचना के चरण : 

(i) एक रंखाखंड BC = 7 cm खींचा ।

(ii) बिंदु B पर 45⁰ का कोण बनाया ।

(iii) बिंदु C पर 30⁰ कोण बनाया क्‍योकि < C = 180⁰– (< A + < B) इस प्रकार हमें ∆ABC प्राप्‍त हुआ ।

(iv) अब BC के नीचे न्‍यून कोण बनाती हुई एक किरण BX खींचा ।

(v) 4 बिंदु (`\frac{4}{3}` में 4 और 3 में स‍बसे बड़ी संख्‍या) B₁, B_2,, B₃ और B₄ किरण BX में इस प्रकार अंकित किया कि कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ हो ।

(vi) B₃ (तीसरा बिंदु `\frac{4}{3}` में 4 और में से छोटी संख्‍या) को C से मिलाया और B₄ से होकर जाने वाली B₃C के समांतर एक रेखा बढ़ाए गए रेखाखंड BC को माना C पर प्रतिच्‍छेद करती हैं।

(vii) अब C से होकर जाने वाली रेखाखंड CA के समांतर एक अन्‍य रंखा बढ़ाई जाने पर रेखाखंड BA को माना A पर प्रतिच्‍छेद करती है खींचा ।
तब ABC अभीष्‍ट त्रिभुज है जो ∆ABC की संगत भुजाओं की `\frac{4}{3}` गुणी हैं।

प्रश्न 7. एक समकोण त्रिभुज की रचना कीजिए जिसकी भुजाएँ (कर्ण के अतिरिक्त) 4 cm व 3 cm लम्बाई की हों। फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की `\frac{5}{3}` गुनी हों।

रचना के चरण : 

(i) एक रेखाखंड BC = 4cm खींचा ।

(ii) बिंदु B पर 90⁰ का कोण बनाया ।

(iii) 90⁰ कोण बनाने वाली किरण BY में से B को केंद्र मानकर और 3cm कि त्रिज्‍या लेकर एक चाप खींचा जो किरण BY को माना बिंदु A पर प्रतिच्‍छेद करती हैं। ।

(iv) AC को मिलाया । इस प्रकार हमें समकोण ∆ABC प्राप्‍त हुआ ।

(v) अब BC के नीचे न्‍युन कोण बनाती हुई एक किरण BX खींचा ।

(vi)5 बिंदु (5/3 में 5 और 3 में से बड़ी संख्‍या) B₁, B_2,, B₃, B₄ और B₅ किरण BX पर इस प्रकार अंकित किया कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ हो ।

(v) B₃ (‍तिसरा बिंदु 5/3 में 5 और 3 में सबसे छोटी संख्‍या) को C से मिलाया और B₅ से होकर जाने वाली B₃C||B₅C खींचा जो बढ़ाए गए BC को बिंदु C पर प्रतिच्‍छेद करती हैं।

(vi) बिंदु C से होकर जानेवाली रेखा CA||CA खींचा जो BA के बढ़ाए गए BA को मान बिंदु A पर प्रतिच्‍छेद करती हैं।
तब ∆ABC ही अभीष्‍ट त्रिभुज है जिसकी प्रत्‍येक भुजा दिए हुए ∆ABC की संगत भुजाओं की 5/3 गुनी हैं।