Mathematics

BSEB Bihar Board Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.2

Bihar Board Class 10 Maths दो चरों वाले रैखिक समीकरण युग्म Ex 3.2

प्रश्न 1. निम्न समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके ग्राफीय विधि से हल ज्ञात कीजिए-
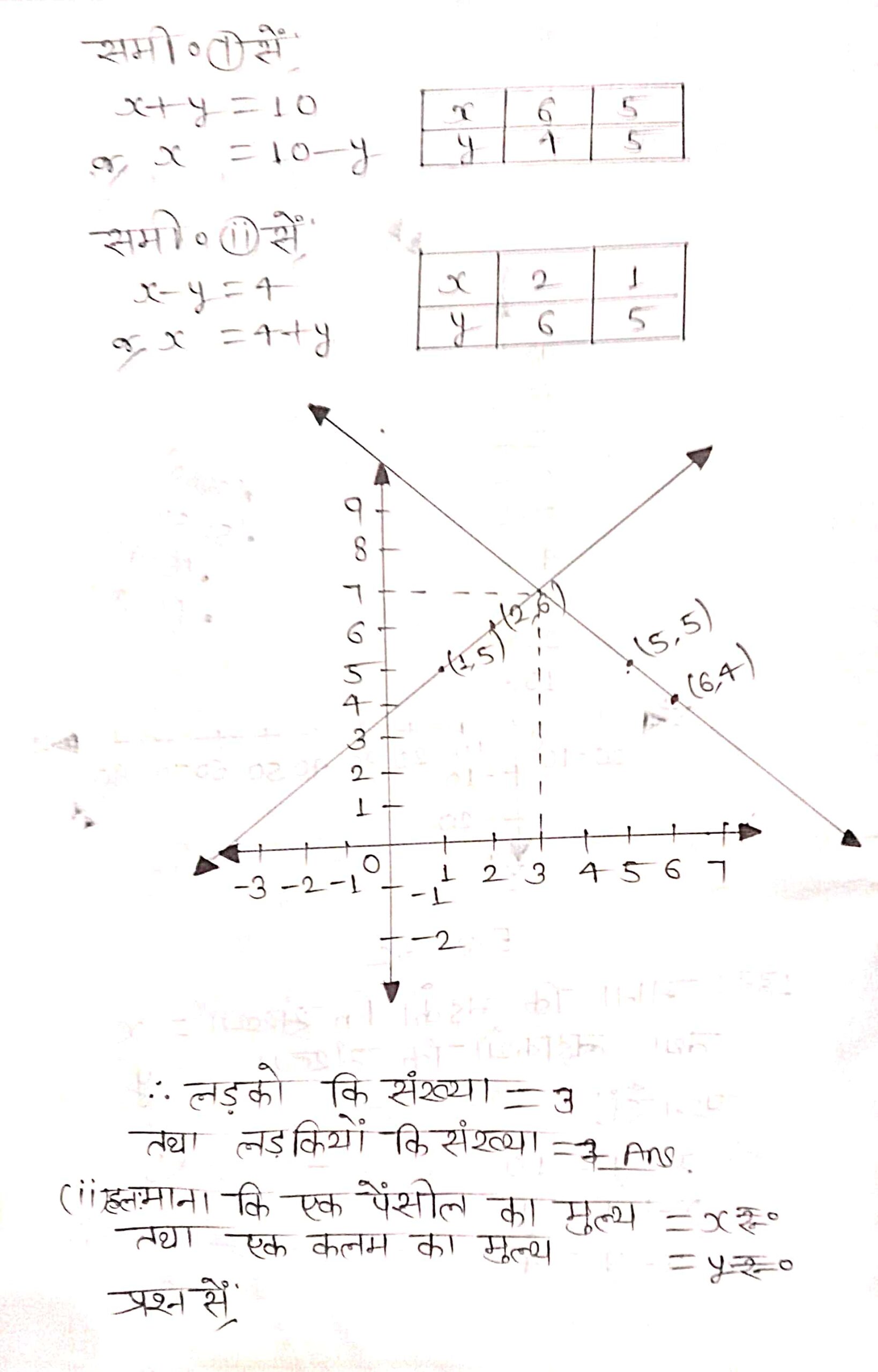
(i) कक्षा X के 10 विद्यार्थियों ने एक गणित की पहेली प्रतियोगिता में भाग लिया। यदि लड़कियों की संख्या लड़कों की संख्या से 4 अधिक हो तो प्रतियोगिता में भाग लिए लड़कों और लड़कियों की संख्या ज्ञात कीजिए।
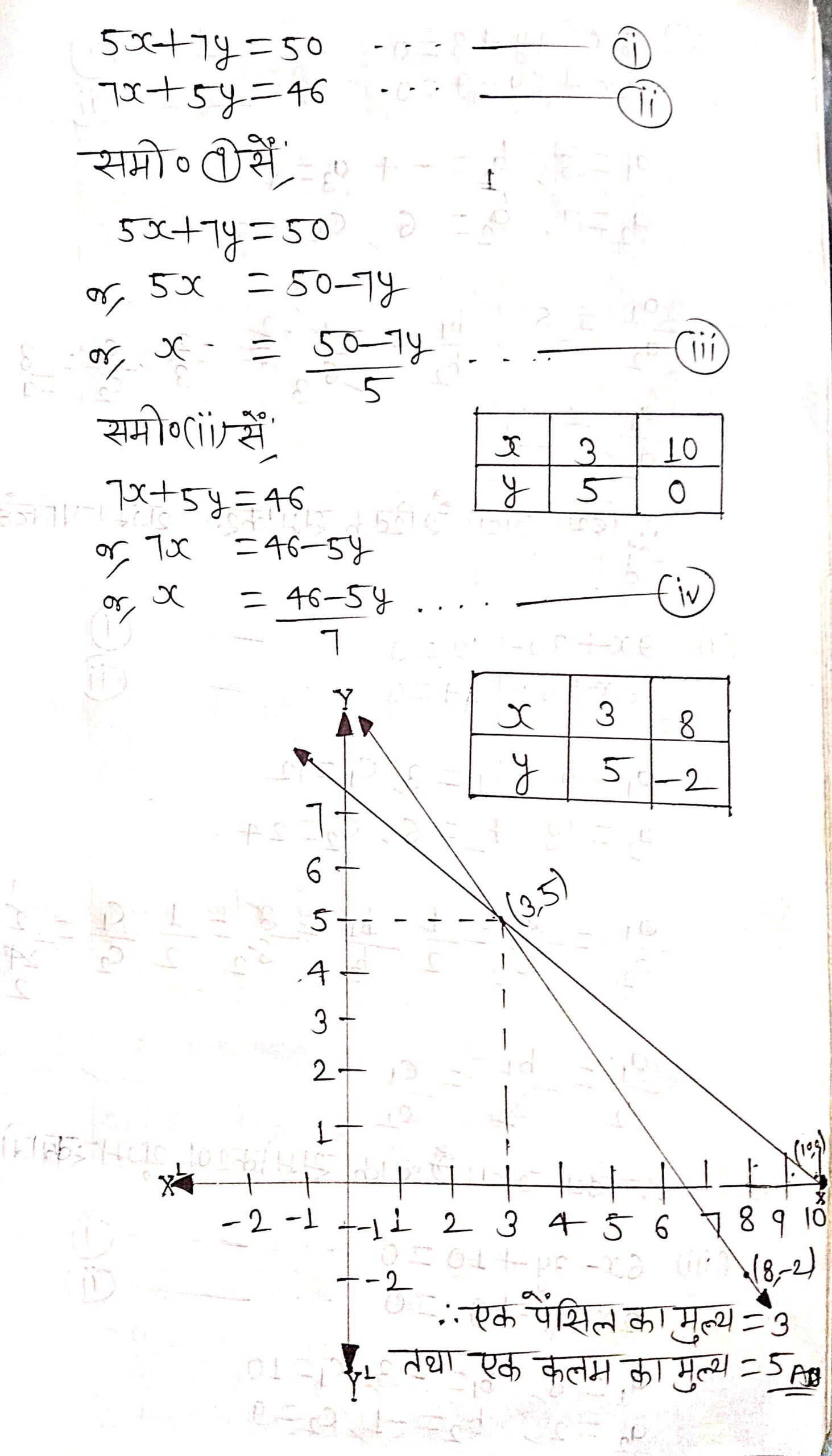
(ii) 5 पेन्सिलों तथा 7 कलमों का कुल मूल्य ₹ 50 है, जबकि 7 पेन्सिलों तथा 5 कलमों का कुल मूल्य ₹ 46 है। एक पेन्सिल का मूल्य तथा एक कलम का मूल्य ज्ञात कीजिए।

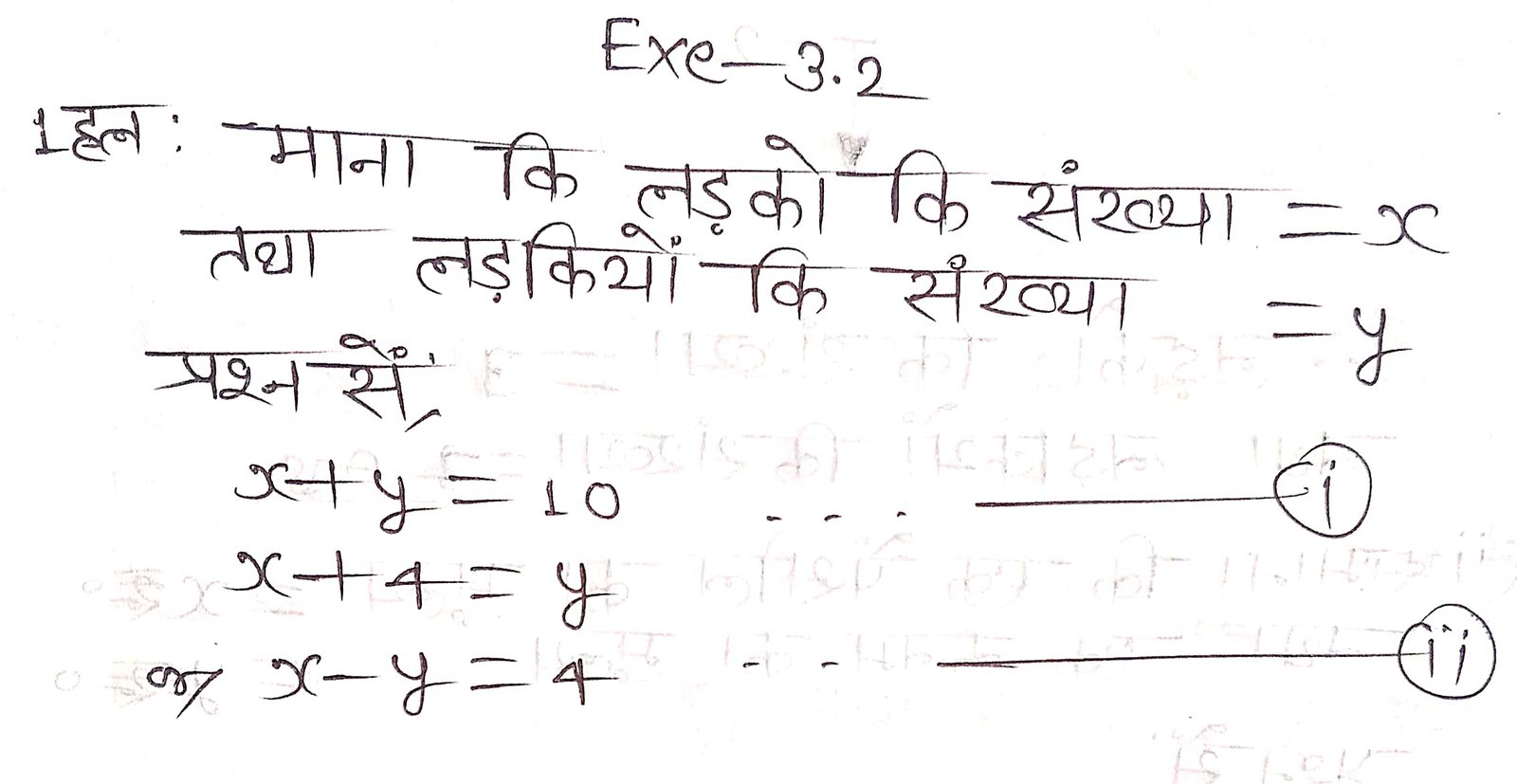
प्रश्न 2.
अनुपातों a1/a2, b1/b2 और c1/c2 की तुलना कर ज्ञात कीजिए कि निम्न समीकरण युग्म द्वारा निरूपित रेखाएँ एक बिन्दु पर प्रतिच्छेद करती हैं, समान्तर अथवा सम्पाती है।

प्रश्न 3. अनुपातों a1a2, b1b2 और c1c2 की तुलना कर ज्ञात कीजिए कि निम्न रैखिक समीकरणों के युग्म संगत हैं या असंगत-
(i) 3x + 2y = 5; 2x – 3y = 7
(ii) 2x – 3y = 8; 4x – 6y = 9
(iii) 32x + 53y = 7; 9x – 10y = 14
(iv) 5x – 3y = 11; -10x + 6y = -22
(v) 43 x + 2y = 8; 2x + 3y = 12

प्रश्न 4. निम्न रैखिक समीकरणों के युग्मों में से कौन-से युग्म संगत/असंगत हैं, यदि संगत हैं तो ग्राफीय विधि से हल ज्ञात कीजिए।
(i) x + y = 5, 2x + 2y = 10
(ii) x – y = 8, 3x – 3y = 16
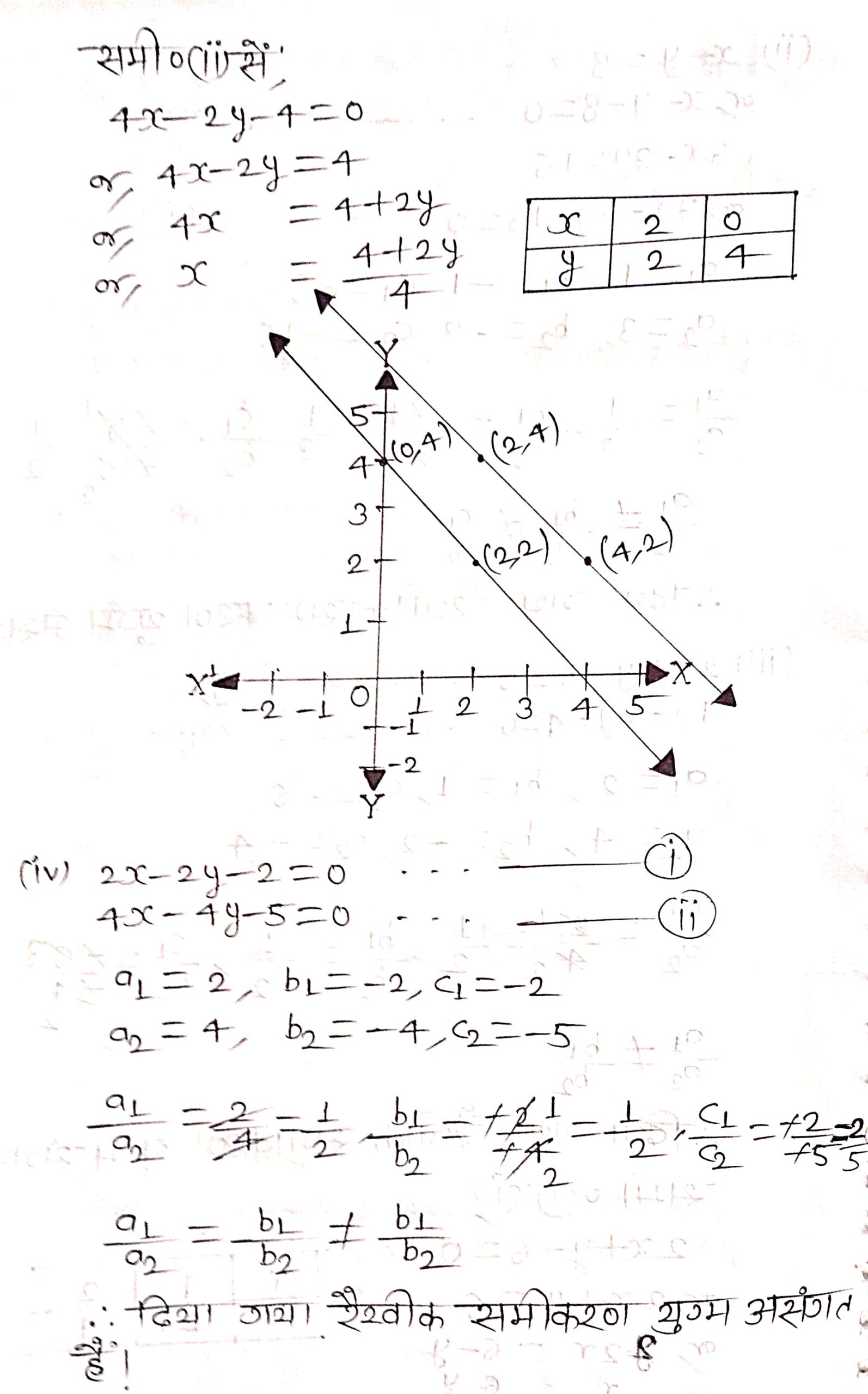
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0

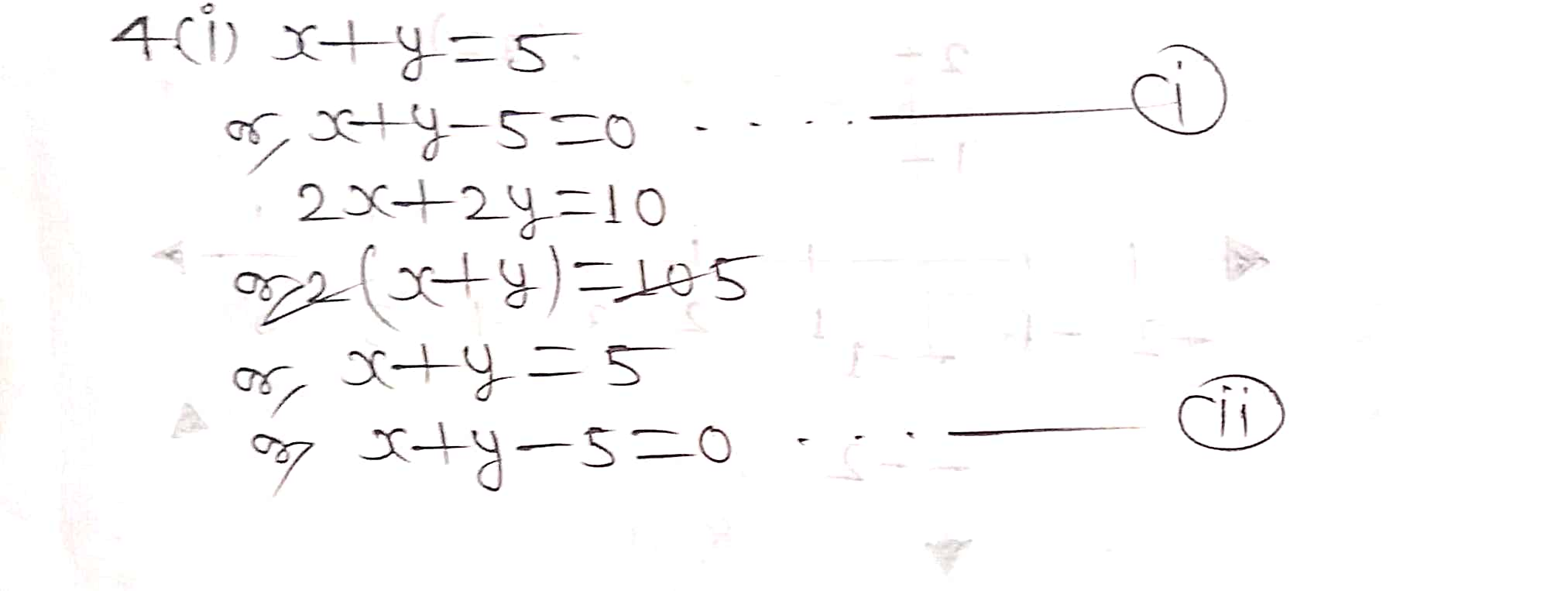
प्रश्न 5. एक आयताकार बाग, जिसकी लम्बाई, चौड़ाई से 4 मीटर अधिक है, का अर्द्धपरिमाप 36 मीटर है। बाग की विमाएँ ज्ञात कीजिए।

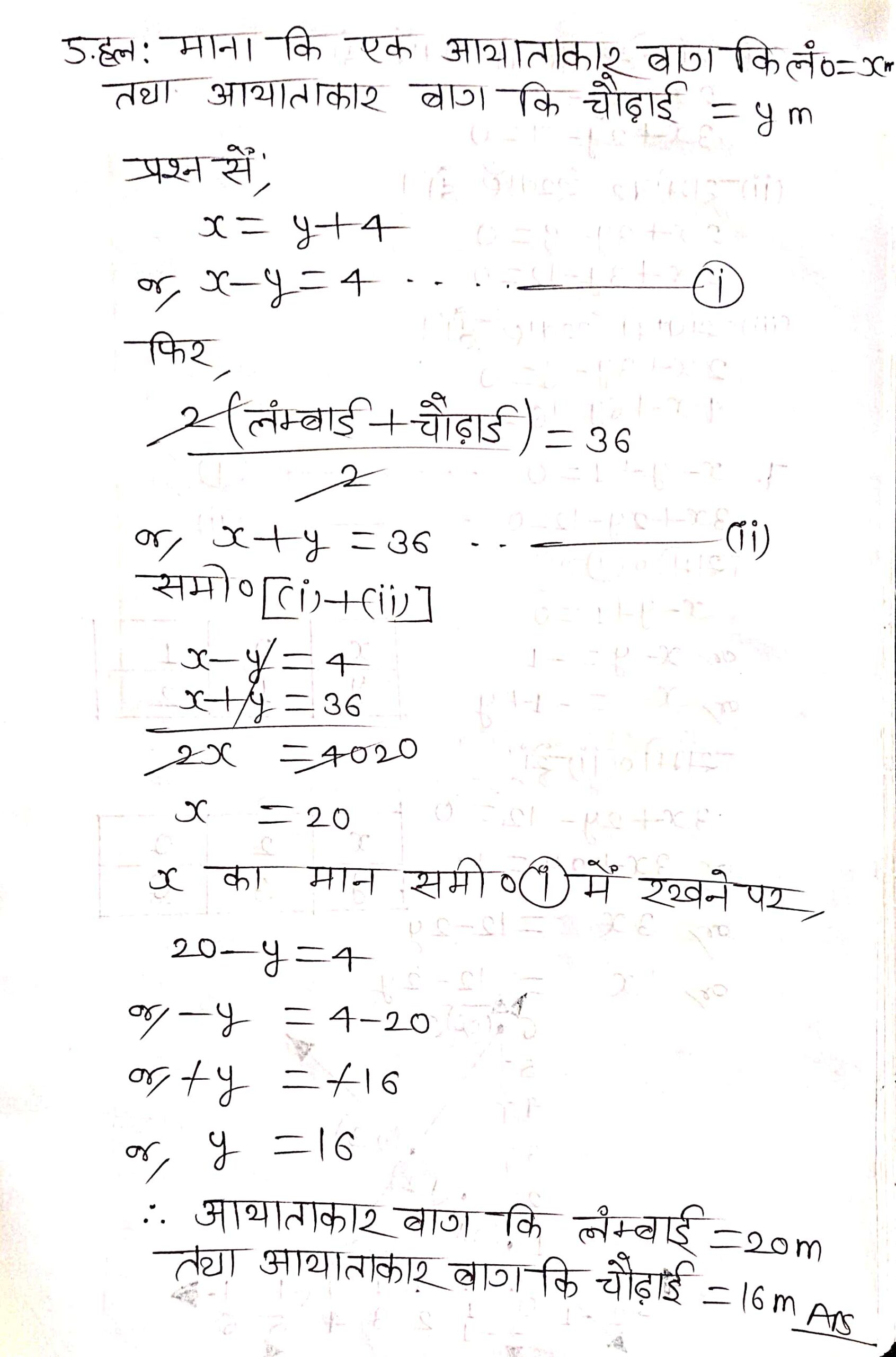प्रश्न 6. एक रैखिक समीकरण 2x + 3y – 8 = 0 दी गई है। दो चरों में एक ऐसी और रैखिक समीकरण लिखिए ताकि प्राप्त युग्म का ज्यामितीय निरूपण जैसा कि
(i) प्रतिच्छेद करती रेखाएँ हों।
(ii) समान्तर रेखाएँ हों।
(iii) सम्पाती रेखाएँ हों।प्रश्न 7. समीकरणों x – y + 1 = 0 और 3x + 2y – 12 = 0 का ग्राफ खींचिए। X-अक्ष और इन रेखाओं से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए और त्रिभुजाकार पटल को छायांकित कीजिए।

BSEB Bihar Board Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.1

Bihar Board Class 10 Maths दो चरों वाले रैखिक समीकरण युग्म Ex 3.1

प्रश्न 1.आफ़ताब अपनी पुत्री से कहता है, ‘सात वर्ष पूर्व मैं तुमसे सात गुनी आयु का था। अब से 3 वर्ष बाद मैं तुमसे केवल तीन गुनी आयु का रह जाऊँगा।’ (क्या यह मनोरंजक है?) इस स्थिति को बीजगणितीय एवं ग्राफीय रूपों में व्यक्त कीजिए।

प्रश्न 2. क्रिकेट टीम के एक कोच ने ₹ 3900 में 3 बल्ले तथा 6 गेंदें खरीदीं। बाद में उसने एक और बल्ला तथा उसी प्रकार की 2 गेंदें ₹ 1300 में खरीदीं। इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए।

प्रश्न 3. 2 किग्रा सेब और 1 किग्रा अंगूर का मूल्य किसी दिन ₹ 160 था। एक महीने बाद 4 किग्रा सेब और 2 किग्रा अंगूर का मूल्य ₹ 300 हो जाता है। इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए।

BSEB Bihar Board Class 10 Maths Solutions Chapter 2 बहुपद Ex 2.3

Bihar Board Class 10 Maths बहुपद Ex 2.3

प्रश्न 1. विभाजन एल्गोरिथ्म का प्रयोग करके, निम्न में p(x) को g(x) से भाग देने पर भागफल तथा शेषफल ज्ञात कीजिए-
(i) p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2
(ii) p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x
(iii) p(x) = x⁴ – 5x + 6, g(x) = 2 – x²

प्रश्न 2. पहले बहुपद से दूसरे बहुपद को भाग करके, जाँच कीजिए कि क्या प्रथम बहुपद द्वितीय बहुपद का एक गुणनखण्ड है-
(i) t² – 3, 2t⁴ + 3t³ – 2t² – 9t – 12
(ii) x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2
(iii) x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1

प्रश्न 3.  3x⁴ + 6x³ – 2x² – 10x – 5 के अन्य सभी शून्यक ज्ञात कीजिए, यदि इसके दो शून्यक √5/3 और  −√5/3 हैं।

प्रश्न 4. यदि x³ – 3x² + x + 2 को एक बहुपद g(x) से भाग देने पर, भागफल और शेषफल क्रमशः x – 2 और -2x + 4 हैं तो g(x) ज्ञात कीजिए।

प्रश्न 5. बहुपदों p(x), g(x), q(x) और r(x) के ऐसे उदाहरण दीजिए जो विभाजन एल्गोरिथ्म को सन्तुष्ट करते हों तथा
(i) घात p(x) = घात q(x)
(ii) घात q(x) = घात r(x)
(iii) घात r(x) = 0

BSEB Bihar Board Class 10 Maths Solutions Chapter 2 बहुपद Ex 2.1

Bihar Board Class 10 Maths बहुपद Ex 2.1

प्रश्न 1. किसी बहुपद p(x) के लिए, y = p(x) का ग्राफ नीचे आकृतियों में दिया है। प्रत्येक स्थिति में, p(x) के शून्यकों की संख्या ज्ञात कीजिए।

(1). शून्यकों की संख्या 0 है

(2). शून्यकों की संख्या 1 है 

(3). शून्यकों की संख्या 3 है 

(4). शून्यकों की संख्या 2 है 

(5). शून्यकों की संख्या 4 है 

(6). शून्यकों की संख्या 3 है

BSEB Bihar Board Class 10 Maths Solutions Chapter 2 बहुपद Ex 2.2

Bihar Board Class 10 Maths बहुपद Ex 2.2

निम्न द्विघात बहुपदों के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच कीजिए-
(i) x² – 2x – 8
(ii) 4s² – 4s + 1
(iii) 6x² – 3 – 7x
(iv) 4u² + 8u
(v) t² – 15
(vi) 3x² – x – 4

प्रश्न 2.एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योगफल तथा गुणनफल क्रमशः दी गई संख्याएँ हैं
(i) 1/4, -1
(ii) √2, 1/3
(iii) 0, √5
(iv) 1, 1
(v) −1/4, 1/4
(vi) 4, 1

BSEB Bihar Board Class 10 Maths Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.4

BSEB Class 10 Maths वास्तविक संख्याएँ Ex 1.4

प्रश्न 1. बिना लम्बी विभाजन प्रक्रिया किए बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत हैं या असांत आवर्ती हैं

प्रश्न 2. उपर्युक्‍त प्रश्‍नों में दी गई उन परिमेय संख्याओं के दशमलव प्रसारों को लिखिए जो सांत हैं-

प्रश्न 3. कुछ वास्तविक संख्याओं के दशमलव प्रसार नीचे दर्शाए गए हैं। प्रत्येक स्थिति के लिए निर्धारित कीजिए कि यह संख्या परिमेय संख्या है या नहीं। यदि यह परिमेय संख्या है और के रूप की है तो के अभाज्य गुणनखण्डों के बारे में आप क्या कह सकते हैं?

BSEB Bihar Board Class 10 Maths Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.3

BSEB Class 10 Maths वास्तविक संख्याएँ Ex 1.3

प्रश्न 1. सिद्ध कीजिए कि √5 एक अपरिमेय संख्या है।

प्रश्न 2. सिद्ध कीजिए कि 3 + 2√5 एक अपरिमेय संख्या है।

प्रश्न 3. सिद्ध कीजिए कि निम्नलिखित संख्याएँ अपरिमेय हैं
(i) 1/√2
(ii) 7√5
(iii) 6 + √2

BSEB Bihar Board Class 10 Maths Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.1

BSEB Class 10 Maths वास्तविक संख्याएँ Ex 1.1

प्रश्न 1. निम्नलिखित संख्याओं का महत्तम समापवर्तक (H.C.F.) ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग कीजिए :
(i) 135 और 225
(ii) 196 और 38220
(iii) 867 और 255

प्रश्न 2. दर्शाइए कि कोई भी धनात्मक विषम पूर्णांक 6q + 1 या 6q + 3 या 6q + 5 के रूप का होता है, जहाँ कोई पूर्णांक है।

प्रश्न 3. किसी परेड में 616 सदस्यों वाली एक सेना (आर्मी) की टुकड़ी को 32 सदस्यों वाले एक आर्मी बैंड के पीछे मार्च करना है। दोनों समूहों को समान संख्या वाले स्तम्भों में मार्च करना है। उन स्तम्भों की अधिकतम संख्या क्या है जिसमें वे मार्च कर सकते हैं?

प्रश्न 4. यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि धनात्मक पूर्णाक का वर्ग किसी पूर्णांक m के लिए 3m या 3m + 1 के रूप का होता है।

प्रश्न 5. यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णांक का घन 9m, 9m + 1 या 9m + 8 के रूप का होता है।

BSEB Bihar Board Class 10 Maths Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.2

BSEB Class 10 Maths वास्तविक संख्याएँ Ex 1.2

प्रश्न 1. निम्नलिखित संख्याओं को अभाज्य गुणनखण्डों के गुणनफल के रूप में व्यक्त कीजिए-
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429

प्रश्न 2. पूर्णांकों के निम्नलिखित युग्मों के महत्तम समापवर्तक (H.C.F.) और लघुत्तम समापवर्त्य (L.C.M.) ज्ञात कीजिए तथा इसकी जाँच कीजिए कि दो संख्याओं का गुणनफल = H.C.F. × L.C.M. है।
(i) 26 और 91
(ii) 510 और 92
(iii) 336 और 54

प्रश्न 3. अभाज्य गुणनखण्डन विधि द्वारा निम्नलिखित पूर्णांकों के H.C.F. और L.C.M. ज्ञात कीजिए :
(i) 12, 15 और 21
(ii) 17, 23 और 29
(iii) 8, 9 और 25

प्रश्न 4. H.C.F. (306, 657) = 9 दिया है। L.C.M. (306, 657) ज्ञात कीजिए।

प्रश्न 5. जाँच कीजिए कि क्या किसी प्राकृत संख्या n के लिए 6ⁿ अंक 0 पर समाप्त हो सकती है?

प्रश्न 6. व्याख्या कीजिए कि 7 × 11 × 13 + 13 और 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 भाज्य संख्याएँ क्यों हैं?

प्रश्न 7. किसी खेल के मैदान के चारों ओर एक वृत्ताकार पथ है। इस मैदान का एक चक्कर लगाने में सोनिया को 18 मिनट लगते हैं, जबकि इसी मैदान का एक चक्कर लगाने में रवि को 12 मिनट लगते हैं। मान लीजिए कि वे दोनों एक ही स्थान और एक ही समय पर चलना प्रारम्भ करके एक ही दिशा में चलते हैं। कितने समय बाद वे पुनः प्रारम्भिक स्थान पर मिलेंगे?