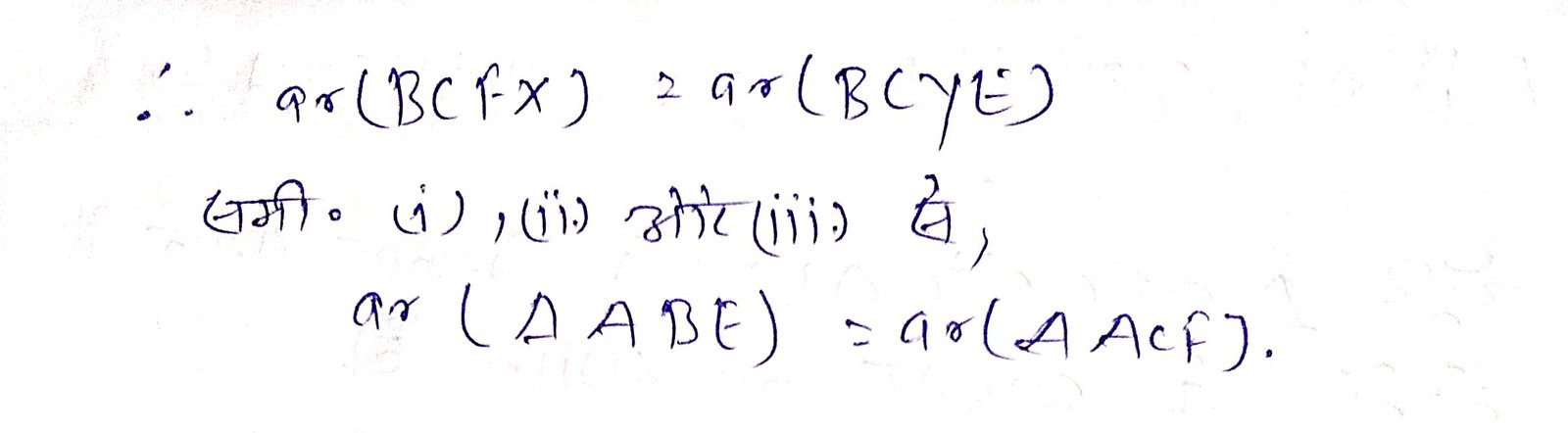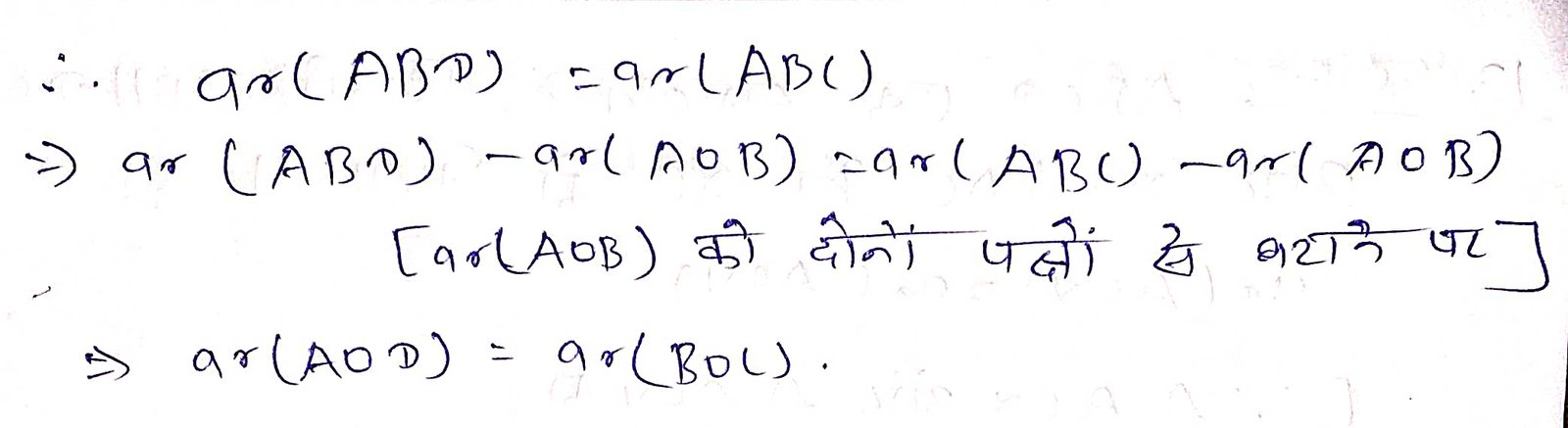प्रश्न 1. 5 cm तथा 3 cm त्रिज्या वाले दो वृत्त दो विन्दुओं पर प्रतिच्छेद करते हैं तथा मके केन्द्रों के बीच की दूरी 4 cm है। उभयनिष्ठ जीवा की लम्बाई ज्ञात कीजिए।.
प्रश्न 2. यदि एक वृत्त की दो समान जीयाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के खण्ड दूसरी जीवा के संगत खण्डों के बराबर है।
प्रश्न 3. बदि एक वृत्त की दो समान जीवाएं वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि प्रतिच्छेद विन्दु को केन्द्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती हैं।
प्रश्न 4. यदि एक रेखा दो संकेन्द्री वृत्तों (एक ही केन्द्र वाले वृत्त) को, जिनका केन्द्र O है. A, B, C और D पर प्रतिच्छेद करे, तो सिद्ध कीजिए AB = CD(पाठ्य-पुस्तक में आकृति देखिए।)
प्रश्न 5. एक पार्क में बने 5 m त्रिज्या वाले बन पर खड़ी तीन लड़कियाँ रेशमा, सलमा एवं मनदीप खेल रही है। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती है। यदि रेशमा तथा सलमा के बीच और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 m झे, तो रेशमा और मनदीप के बीच की दूरी क्या है?
प्रश्न 6. 20 m त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कालोनी में स्थित है। तीन लड़के अंकुर, सैय्यद तथा डेविड इसकी परिसीमा पर बराबर दूरी पर बैठेहैं और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है। प्रत्येक फोन की डोरी की लम्बाई ज्ञात कीजिए।
प्रश्न 1. याद कीजिए कि दो वृत्त सर्वागतम होते हैं, यदि उनकी त्रिज्याएं बराबर हो। सिद्धकीजिए कि सर्वांगसम वृत्तों की बराबर जीयाएँ उनके केन्द्रों पर बराबर कोण अंतरित करती हैं।
प्रश्न 2. सिद्ध कौजिए कि यदि सर्वागसम वृत्तों की जीवाएं उनके केन्द्रों पर बराबरकोण अंतरित करें, तो जीवाएँ बराबर होती हैं।
प्रश्न 1. खाली स्थान भरिए (i) वृत्त का केन्द्र वृत्त के …………. मैं स्थित है। (बहिभाग अभ्यंतर) (ii) एक बिन्दु, जिसकी वृत्त के केन्द्र से दूरी जिऱ्या से अधिक हो वृत्त के …………. स्थित होता है (बहिभाग अभ्यंतर) (iii) वृत्त की सबसे बड़ी जीया वृत्त का ………….. होता हो। (iv) एक चाप ……………. होता है, जब इसके सिने एक व्यास के सिरे हो। (v) वृत्तबग्ह एक चाप तथा …………… के बीच का भाग हो। (vi) एक वृत्त, जिसके तल पर स्थित है, उसे ……………… भागों में विभाजित करता है।
1. हल – (i) अभ्यंतर (ii) बहिर्भाग (iii) व्यास (iv) अर्ध गोला (v) एक जीवा (vi) तीन ।
प्रश्न 2. लिखिए, सत्स वा असत्य। अपने उत्तर के कारण दीजिए। (i) केन्द्र को वृत्त पर किसी बिन्दु से मिलाने वाला रेखाखण्ड वृत्त की त्रिज्या होती है। (ii) एक वृत्त में समान लम्बाई की परिमित जोगाएँ होती है। (iii) यदि एक वृत्त को तीन बराबर चापों में बाँट दिया जाए, तो प्रत्येक भाग दीर्घ चाप होता है। (iv) वृत की एक जीया, जिसकी लम्बाई त्रिज्या से दो गुनी हो. वृत्त का व्यास है। (v) त्रिन्यखंड, जौवा एवं संगत चाप के बीच का क्षेत्र होता (vi) वृत्त एक समतल आकृति है।
प्रश्न 1. आकृति में, ∆ABC की एक माध्यिका AD पर स्थित E कोई विन्दु है। दर्शाइए कि ar (∆ABE) = ar (∆ACE) है।
प्रश्न 2. ∆ABC में, E माध्यिका AD का मध्य बिन्दु है। दर्शाइए कि ar (∆BED) = 1/4 ar (∆ABC) है।
प्रश्न 3. दर्शाइए कि समानर चतुर्भुज के दोनों विकर्ण असे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बांटते हैं।
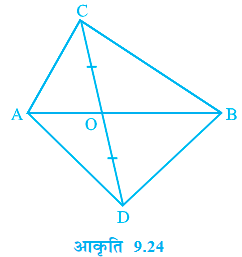
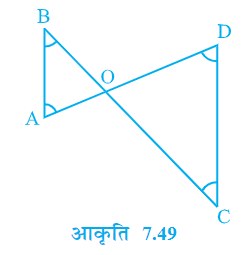
प्रश्न 4. आकृति में, ABC तथा ABD एक ही आधार AB पर बने दो त्रिभुज हैं। यदि रेखाखण्ड CD रेखाखण्ड AB बिन्दु O पर समद्वि भाजित होता है, तो दर्शाइए कि ar (ABC) = ar (ABD) है।
प्रश्न 5. D, E और Fक्रमशः त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य बिन्दु हैं। दर्शाइए कि-
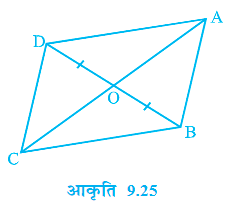
प्रश्न 6. पाठ्य पुस्तक में दी गई आकृति में, चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु ० पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है। यदि AB = CD है, तो दहिए कि- (i) ar (DOC) = ar(AOB) (ii) ar (DCB) = ar (ACB) (iii) DA ||CB या ABCD एक समान्तर चतुर्भुज है।
प्रश्न 7. विन्दु D और E क्रमश: ∆ABC की भुजाओं AB और AC पर इस प्रकार स्थित है कि ar (∆DBC) = ar (∆EBC) है। दर्शावए कि DE || BC है।
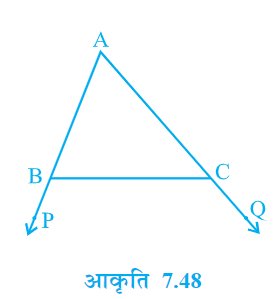
प्रश्न 8. XY त्रिभुज ABC की भुजा BC के समानतर एक रेखा है। यदि BE || AC और CF || AR रेखा XY से क्रमश: E और F पर मिलती हैं, तो दर्शाइए कि–ar (∆ABE) = ar (∆ACF).
प्रश्न 9. समान्तर चतुर्भुज ABCD की एक भुजा AB को एक बिन्दु तक बढ़ाया गया है। A से होकर CP के समान्तर खींची गई रेखा बढ़ाई गई CB को Q ए पर मिलती है और फिर समान्तर चतुर्भुज PBQR को पूरा किया गया है (पाठ्य पुस्तक में आकृति देखिए)। दर्शाइए कि
प्रश्न 10. एक समलम्ब ABCD, जिसमें AB || DC है. के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि ar (∆AOD) = ar (∆BOC) है।
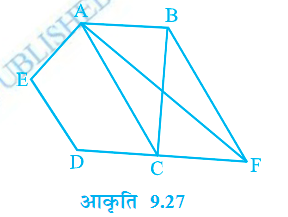
प्रश्न 11. आकृति में, ABCDE एक पचभुज है। B से होकर AC के समान्तर खींची गई रेखा बढ़ाई गई DC को F पर मिलती है। दर्शाइए कि- (i) ar (∆ACB) = ar (∆ACF) (ii) ar (AEDF) = ar (ABCDE).
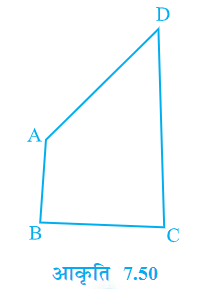
प्रश्न 12. गाँव के एक निवासी इतवारी के पास एक चतुभुजाकार भूखण्ड था। उस गाँव की ग्राम पंचायत ने उसके भूखण्ड के एक कोने से उसका कछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केन्द्र का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस प्रतिबन्ध के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखण्ड के संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखण्ड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है।
प्रश्न 13. ABCD एक समलम्य है, जिसमें AB || DC है। AC के समान्तर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है। सिद्ध कीजिए कि ar (ADX) = ar (ACY) है।
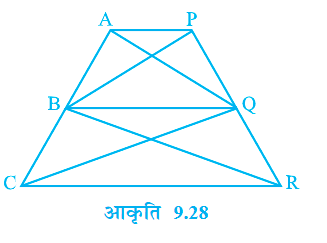
प्रश्न 14. आकृति में AP || BQ || CR है। सिद्ध कीजिए कि ar (AQC) = ar (PBR) है।
प्रश्न 15. चतुर्भुज ABCD के विकणं AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते है कि ar (∆AOD) = ar (∆BOC) है। सिद्ध कीजिए कि ARCD एक समलम्य है।
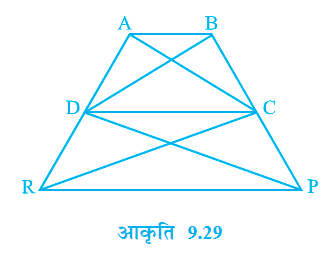
प्रश्न 16. आकृति में ar (∆DRC) = ar (∆DPC) है और ar (∆BDP) = ar (∆ARC) है। दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलम्ब हैं।
प्रश्न 1. आकृति में, ABCD एक समान्तर चतुर्भुज है: AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 cm, AE = 8cm और CF = 10 cm है, तो AD जात कीजिए।
प्रश्न 2. यदि E, F, G और H क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं के मध्य-बिन्दु है, तो दर्शाइए कि ar (EFGH) = 12 ar (ABCD) है।
प्रश्न 3. P और Q क्रमशः समानर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित बिन्दु हैं। दर्शाइए कि ar (APB) = ar (BQC) है।
प्रश्न 4. पाठ्य पुस्तक में दी गई आकृति में, P समाजर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिन्दु है। दर्शाइए कि- (i) ar (APB) + ar (PCD) = 1/2 ar (ABCD) (ii) ar (APD)+ar (PBC) = ar (APB) + ar (PCD)
प्रश्न 5. आकृति में, PQRS और ABRS समान्तर चतुर्भुज हैं तथा x भुजा BR पर निश्चत कोई बिन्दु है। दांडए कि- (i) ar (PQRS) = ar (ABRS) (ii) ar (AXS) = 1/2 ar (PQRS)
प्रश्न 6. एक किसान के पास समाजर चतुर्भुज PQRS के रूप का एक खेत था। उसने RS पर स्थित कोई बिन्दु A लिया और उसे P और Q से मिला दिया। खेत कितने भागों में विभाजित हो गया है? इन भागों के आकार क्या हैं? वह किसान खेत में गेहूँ और दालें बराबर-बराबर भागों में अलग-अलग बोना चाहता है। वह ऐसा कैसे करे?
प्रश्न 1. पाठ्य पुस्तक में दी गई आकृतियों में कौन-सी आकृतियाँ एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित हैं? ऐसी स्थिति में,जभवनिष्ठ आधार और दोनों समान्तर रेखाएं लिखिए।
प्रश्न 1. ABCD एक चतुर्भुज है जिसमें POR और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं (देखिए आकृति) AC उसका एक विकर्ण है। दर्शाइए कि- (i) SR || AC और SR = 1/2 AC है। (ii) PQ = SR है। (iii) RQRS एक समान्तर चतुर्भुज है।
प्रश्न 2. ABCD एक समचतुर्भुज है और P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य विन्दु हैं। दशहिए कि चतुर्भुज PQRS एक आयत है।
प्रश्न 3. ABCD एक आयत है, जिसमें P, Q, R और S क्रमश: AB, BC, CD और DA के मध्य विन्दु हैं। दर्शाइए कि चतुर्भुज PQRS एक समचतुर्भुज है।
प्रश्न 4. ABCD एक समलम्ब है, जिसमें AB || DC है। साथ ही, BD एक विकर्ण है और E भुजा AD का मध्य बिन्दु है। E से होकर एक रेखा AB के सपाजर खींची गई है, जो BC को F पर प्रतिच्छेद करती है (पाठ्य पुस्तक में आकृति देखिए)। दर्शाइए किा भुजा BC का मध्य-बिन्दु है।
प्रश्न 5. एक समान्तर चतुर्भुज ABCD में E और F क्रमशः भुजाओं AB और CD के मध्य-बिन्दु हैं(देखिए आकृति) दशाइए कि रेखाखण्ड AF तथा EC विकर्ण BD को समविभाजित करते हैं।
प्रश्न 6. दर्शाइए कि किसी चतुर्भुज की सम्मुख भुजाओं के मध्य बिन्दुओं को मिलाने वाले रेखाखण्ड परस्पर समद्विभाजित करते हैं।
प्रश्न 7. ABC एक त्रिभुज है जिसका ∠C समकोण है। कर्ण AB के मध्य बिन्दु M से होकर RC के समान्तर खींची गई रेखा AC को D पर प्रतिच्छेद करती है। दर्शाइए कि- (i) D भुजा AC का मध्य विन्दु है। (b) MD ⊥ AC है। (iii) CM = MA = 1/2AB है।
प्रश्न 1. एक चतुर्भुज के कोण 3 : 5 : 9 : 13 के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए।
प्रश्न 2. बदि एक समाजर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है।
प्रश्न 3. दर्शाइए कि यदि एक चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करें, तो वह एक समचतुर्भुज होता है।
प्रश्न 4. दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
प्रश्न 5. दाइए कि यदि एक चतुर्भुज के विकर्ण बराबर हों और परस्पर लम्बवत् समद्विभाजित करें, तो वह एक वर्ग होता है।
प्रश्न 6. समान्तर चतुर्भज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है (देखिए आकृति)। वशाईए कि- (i) यह को भी समद्विभाजित करता है। (ii) ABCD एक समचतुर्भुज है।
प्रश्न 7. ABCD एक समचतुर्भुज है। दर्शाइए कि विकर्ण AC, ∠A और ∠C दोनों को समद्विभाजित करता है तथा विकर्ण BD, ∠B और ∠D दोनों को समद्विभाजित करता है।
प्रश्न 8. ABCD एक आयत है जिसमें विकर्ण AC दोनों ∠A और ∠C को समद्विभाजित करता है। दर्शाइए कि (i) ABCD एक वर्ग है (ii) विकर्ण BD, दोनों ∠B और ∠D को समद्विभाजित करता है।
प्रश्न 9. समानर चतुर्भुज ABCD के विकणं BD पर दो बिन्दु P और Q इस प्रकार स्थित हैं कि DP = BQ है। (पाठ्य पुस्तक में दी गई आकति) वांडा कि- (i) ∆APD ≅ ∆COB (ii) AP = CQ (iii) ∆AQB ≅ ∆CPD (iv) AQ = CP
प्रश्न 10. ABCD एक समानार चतुर्भुज है तथा AP और CQ शीघों A और C से विकर्ण BD पर क्रमशः लम्ब हैं(देखिए आकृति)। वर्शाइए कि- (i) ∆APB ≅ ∆CQD (ii) AP= CQ.
प्रश्न 11. ∆ABC और ∆DEF में, AB = DE. AB || DE, BC = EF और BC || EF है। शीर्षों A, B और C को क्रमशः शीपों D, E और F मै जोडा जाता है। (देखिए आकृति)। दहिए कि- (i) चतुर्भुज ABED एक समान्तर चतुर्भुज है। (ii) चतुर्भुज BEFC एक समान्तर चतुर्भज है। (iii) AD || CF और AD = CE है। (iv) चतुर्भुज ACFD एक समान्तर चतुर्भुज है। (v) AC = DF है। (vi) ∆ABC = ∆DEF है।
प्रश्न 12. ABCD एक समलम्ब है जिसमें AB || DC और AD = BC (देखिए आकृति) दर्शाइए कि- (1) ∠A = ∠B (ii) ∠C = ∠D (iii) ∆ABC ≅ ∆BAD (iv) विकर्ण AC = विकणं BD है।
प्रश्न 1. दर्शाइए कि समकोण त्रिभुज में कर्ण सबसे लम्बी भुजा होती है।
प्रश्न 2. आकृति में, ∆ABC की भुजाओं AB और AC को क्रमशः बिंदुओं P और Q तक बढ़ाया गया है। साथ ही, ∠PDC < ∠QCB है। दर्शाइए कि AC > AB है।
प्रश्न 3. आकृति में, ∠B < ∠A और ∠C < ∠D है। दर्शाइए कि AD < BC है।
प्रश्न 4. AB और CD क्रमशः एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजाएँ है (देखिए पाठ्य पुस्तक में आकृति)। दर्शाइए कि ∠A > ∠C और ∠B > ∠D है।
प्रश्न 5. आकृति में, PR > PQ है और PS कोण QPR को समद्विभाजित करता है। सिद्ध कीजिए कि ∠PSR > ∠PSQ है।
प्रश्न 6. दर्शाइए कि एक रेखा पर एक दिए हुए विन्दु मे.जो उस रेखा पर स्थित नहीं है, जितने रेखाखण्ड खींचे जा सकते हैं उनमें लम्य रेखाखण्ड सबसे छोटा होता है।
